Expliquer les structures en maillons des jets d’eau
Si l’on verse lentement l’eau contenue dans un verre ordinaire, on observe un phénomène surprenant : la colonne d’eau est composée d’une série de « maillons » verticaux d’axe horizontal se succédant l’un après l’autre avec une rotation de 90° entre eux. (Fig.1 ci-dessous).

Fig.1. Ecoulement d’eau en sortie d’une bouteille :
On observe des oscillations en maillons quand la
section transverse de départ est non circulaire comme
on le remarque sur la ligne pointillée jaune.
Tiré de Chain oscillations in liquid jets Daniel T. A. Jordan, Neil M. Ribe, Antoine Deblais, and Daniel Bonn PHYSICAL REVIEW FLUIDS 7, 104001 (2022). Avec autorisation.
On peut observer le même effet avec un jet liquide tombant d’un ajutage elliptique ou de toute autre section non circulaire, c’est-à-dire non axisymétrique. Il faut pour cela que les viscosités du jet et du fluide ambiant soient basses et que l’interface ait une tension superficielle élevée. Des jets d’eau dans l’air remplissent ces conditions.
On observe plusieurs « maillons » avant que le jet ne se brise.
Les premières études expérimentales montraient que la longueur d’onde correspondant à l’oscillation des maillons augmentait avec la vitesse v du jet.
En 1879, Rayleigh analysa les perturbations de la surface d’un jet non axisymétrique et trouva qu’elles avaient la forme d’oscillations stables. Mais le phénomène était loin d’être entièrement compris.
Des physiciens du van der Waals Institute, IoP, University of Amsterdam, Pays–Bas et du laboratoire FAST, Université Paris-Saclay, Orsay, France viennent de montrer expérimentalement que la longueur d’onde et l’amplitude des maillons de la chaîne étaient directement liées à la taille de l’ouverture à travers laquelle le liquide coule.
La déformation et la vibration du jet sont des phénomènes dus à la tension superficielle qui tend à réduire la surface du jet.
Si la section du jet est circulaire, les forces de tension superficielle sont axisymétriques et ne modifient pas sa forme cylindrique.
Au contraire, quand la section du jet n’est pas circulaire, ses segments fortement courbés sont poussés vers l’intérieur et ses segments faiblement courbés vers l’extérieur. Ceci entraîne des vibrations horizontales de la section transverse du jet de liquide.
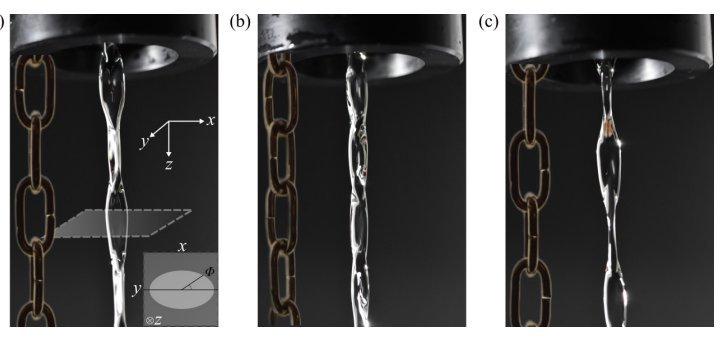
Fig. 2. Géométrie de chaînes liquides et métalliques.
Chacune des 3 images ci-dessus est séparée de la précédente par une rotation de 45°autour de l’axe vertical. L’insert en (a) montre une section du jet à une hauteur z donnée.
Tiré de Chain oscillations in liquid jets Daniel T. A. Jordan, Neil M. Ribe, Antoine Deblais, and Daniel Bonn PHYSICAL REVIEW FLUIDS 7, 104001 (2022). Avec autorisation.
Les fréquences d’oscillations mesurées à partir de la structure de la chaîne de maillons ne correspondaient pas à celles prédites par la théorie de Rayleigh (1879). D. Bonn et al. ont montré que la théorie non linéaire élaborée 30 ans plus tard par N. Bohr (1909) était plus adaptée aux résultats expérimentaux. L’ agrément de cette théorie avec les expériences montre que les chaînes de liquide sont bien des oscillations non linéaires dont la fréquence diminue si leur amplitude augmente. Cette théorie prédit très bien les fréquences mais donne cependant des amplitudes un peu trop fortes par rapport à l’expérience.
Les chercheurs ont alors effectué des simulations numériques. En utilisant le code dit de volume de fluide basé sur une discrétisation du jet et les équations hydrodynamiques de Navier-Stokes, ils ont obtenu un excellent accord avec l’expérience tant en fréquence qu’en amplitude.
.
La figure ci-dessous compare un écoulement expérimental avec le résultat de la théorie de N. Bohr et avec celui de la simulation numérique. L’accord est excellent dans ce dernier cas.
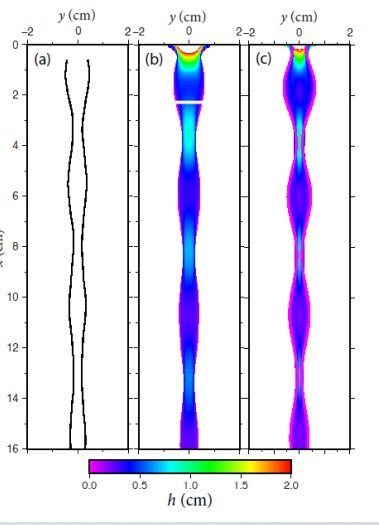
Fig.3. Forme et épaisseur h d’un jet de débit
Q =1,41 l/min tombant d’un ajutage elliptique
de petit axe 1,5 cm et de grand axe 3,0 cm.
Le grand axe est perpendiculaire au plan de la page.
a) Forme du jet observé dans l’expérience.
b) Forme et épaisseur h du jet simulé numériquement.
La partie blanche près du sommet correspond
à une épaisseur 2,0 < h <3,0 cm.
c) Forme et épaisseur du jet prédit par la théorie de Bohr.
On obtient un très bon accord sur les fréquences, mais il est moins bon pour l’amplitude.
Tiré de Chain oscillations in liquid jets Daniel T. A. Jordan, Neil M. Ribe, Antoine Deblais, and Daniel Bonn PHYSICAL REVIEW FLUIDS 7, 104001 (2022). Avec autorisation.
La dynamique des jets sortant d’ajutages non-circulaires présente un intérêt, non seulement en physique fondamentale, mais encore pour de nombreuses applications pratiques. Comme par exemple le mélange de liquides tant à une petite échelle qu’à une grande, l’optimisation de la combustion de liquides, la suppression de bruits et le contrôle de la poussée des moteurs de fusées
Pour en savoir plus :
Chain oscillations in liquid jets Daniel T. A. Jordan, Neil M. Ribe, Antoine Deblais, and Daniel Bonn PHYSICAL REVIEW FLUIDS 7, 104001 (2022)