Première observation d’oscillations stables du ressaut hydraulique
Quand un jet de liquide tombe sur une surface horizontale, ce qu’on observe souvent dans un évier de cuisine, il peut se produire une discontinuité dans l’épaisseur du fluide : à une certaine distance Rj du jet, il y a une augmentation brutale de l’épaisseur du fluide qui entraîne une diminution de la vitesse moyenne du liquide.
On observe alors un cercle de liquide de faible épaisseur entouré d’une couronne plus épaisse.
Cette discontinuité est appelée ressaut hydraulique et a été analysée par Rayleigh en 1914. Cette expérience simple à réaliser ne l’est pas à interpréter et de nombreuses théories cherchent toujours à en donner un modèle complet.
Des chercheurs de l’université de Lille, France, se sont intéressés aux régimes à faible flux liquide et ont observé des instabilités devenant, dans une étroite fenêtre de paramètres, des oscillations périodiques stables observées pour la première fois dans ce phénomène.
Ils ont utilisé un jet d’eau très fin, créé par passage dans une aiguille de diamètre intérieur d, arrivant verticalement sur un disque horizontal en Altuglas, placé à 1 cm de la sortie de l’aiguille.
La figure 1 représente une coupe du ressaut hydraulique par un plan vertical contenant le jet :
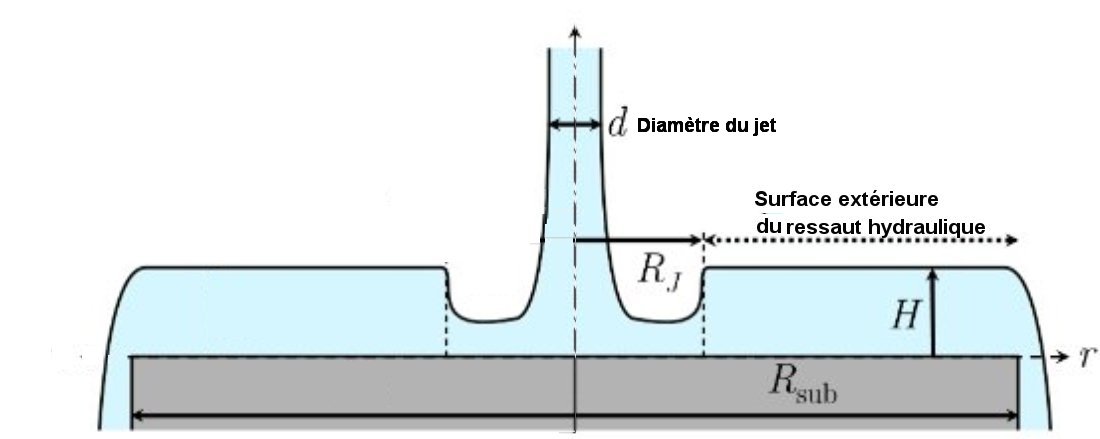
Fig.1. Schéma du profil d’un ressaut hydraulique
Rj est le rayon du ressaut, Rsub celui du disque d’Altuglas,
H est l’épaisseur de la partie extérieure du ressaut ; elle est supérieure à celle de la partie centrale ; d est le diamètre du jet.
Tiré de Oscillations and Cavity Modes in the Circular Hydraulic Jump
Aurélien Goerlinger, Michael Baudoin, Farzam Zoueshtiagh, and Alexis Duchesne PHYSICAL REVIEW LETTERS 131, 194001 (2023) DOI : 10.1103/PhysRevLett.131.194001) Avec autorisation.
La photographie suivante montre l’un des ressauts hydrauliques stationnaires observés par les chercheurs

Fig.2. Photographie d’un ressaut hydraulique
Le diamètre du jet d’eau est ici de 0,9 mm.
La barre blanche d’échelle vaut 1 cm.
Tiré de Oscillations and Cavity Modes in the Circular Hydraulic Jump
Aurélien Goerlinger, Michael Baudoin, Farzam Zoueshtiagh, and Alexis Duchesne PHYSICAL REVIEW LETTERS 131, 194001 (2023) DOI : 10.1103/PhysRevLett.131.194001). Avec autorisation.
Le ressaut hydraulique débute habituellement à partir d’un débit minimum où apparaît la discontinuité, l’augmentation du débit entraînant celle du rayon Rj .
Aurélien Goerlinger et al. se sont intéressés au domaine proche du déclenchement du ressaut en utilisant un jet de débit très stable, allant de 2 à 3 ml/s, attaquant un disque en Altuglas de rayon Rsub allant de 2 à 3 cm. On qualifie parfois le phénomène dans ces conditions de micro ressaut hydraulique.
Avec le plus haut débit utilisé (~3 ml/s) on observe des ressauts hydrauliques stables avec un rayon Rj constant, quel que soit le rayon du disque utilisé.
En diminuant le débit, un état transitoire apparaît où le rayon Rj du ressaut oscille entre 0 et un maximum durant quelques douzaines de secondes avant de finalement retrouver un état stationnaire avec un rayon Rj fini et stable.
Pour des débits autour de 2,5 ml/s et des rayons Rj > 2 cm, on observe un état bistable avec deux comportements stables sous les mêmes conditions, soit l’un avec des oscillations périodiques stables, soit l’autre avec un ressaut hydraulique stable.
Enfin, avec un débit < 2,2 ms/l, l’état bistable précédent disparaît et on observe un état stable d’oscillations périodiques du ressaut dont on peut voir un exemple sur la vidéo ci-dessous :
Video. Oscillations d’un ressaut hydraulique observé par en dessous
Le ressaut est créé par un jet vertical d’eau désionisée de 0,9 mm de diamètre arrivant au centre d’un disque d’Altuglas de 4,5 cm de rayon. Le débit est de 2,1 ml/s. la surface observée vaut 3,8 cm de largeur sur 2,1 cm de haut.
Tiré de Oscillations and Cavity Modes in the Circular Hydraulic Jump
Aurélien Goerlinger, Michael Baudoin, Farzam Zoueshtiagh, and Alexis Duchesne PHYSICAL REVIEW LETTERS 131, 194001 (2023) DOI : 10.1103/PhysRevLett.131.194001). Avec autorisation.
Si on abaisse le débit au dessous de 1,8 ml/s, le ressaut hydraulique après s’être ouvert quelques rares fois au début de l’expérience, cesse définitivement d’exister.
L’analyse des données révèle que la période des oscillations stables ne dépend pas de la valeur du débit même si celui-ci conditionne leur survenue.
La période montre une dépendance linéaire avec le rayon
Rsub du disque substrat ( Fig.3).

Fig.3. Variation de la période T des oscillations en fonction du rayon Rj du disque.
La droite en tirets pourpre correspond au fit linéaire des périodes fondamentales, celle en tirets bleus correspond aux périodes harmoniques.
Tiré de Oscillations and Cavity Modes in the Circular Hydraulic Jump
Aurélien Goerlinger, Michael Baudoin, Farzam Zoueshtiagh, and Alexis Duchesne PHYSICAL REVIEW LETTERS 131, 194001 (2023) DOI : 10.1103/PhysRevLett.131.194001). Avec autorisation.
Les points expérimentaux se groupent sur deux droites de pentes différentes définissant 2 modes d’oscillations. Dans les mêmes conditions expérimentales, la période observée est l’une de ces 2 valeurs.
Pour interpréter cela, les physiciens ont fait l’hypothèse que des ondes de gravité de surface étaient émises dans la cavité limitée par l’epaisse région extérieure du ressaut.
En utilisant un modèle théorique des modes de la cavité, ils ont trouvé que les ondes dans la cavité sont représentées par des fonctions de Bessel. On obtient un parfait agrément avec la valeur expérimentale de 0,54 (Fig.3) du rapport des pentes des deux droites de la fig.3.
Les chercheurs ont démontré que les oscillations avaient leur origine dans le couplage entre des modes d’ondes de surface et le ressaut hydraulique. Ils ont aussi montré que deux ressauts hydrauliques pouvaient osciller de façon synchrone en opposition de phase si ils sont placés à une distance particulière.
Cette découverte peut ouvrir la voie à l’exploration d’interactions complexes entre des ondes de surface et de multiples ressauts oscillants.
Pour en savoir plus :
Oscillations and Cavity Modes in the Circular Hydraulic Jump
Aurélien Goerlinger, Michael Baudoin, Farzam Zoueshtiagh, and Alexis Duchesne
PHYSICAL REVIEW LETTERS 131, 194001